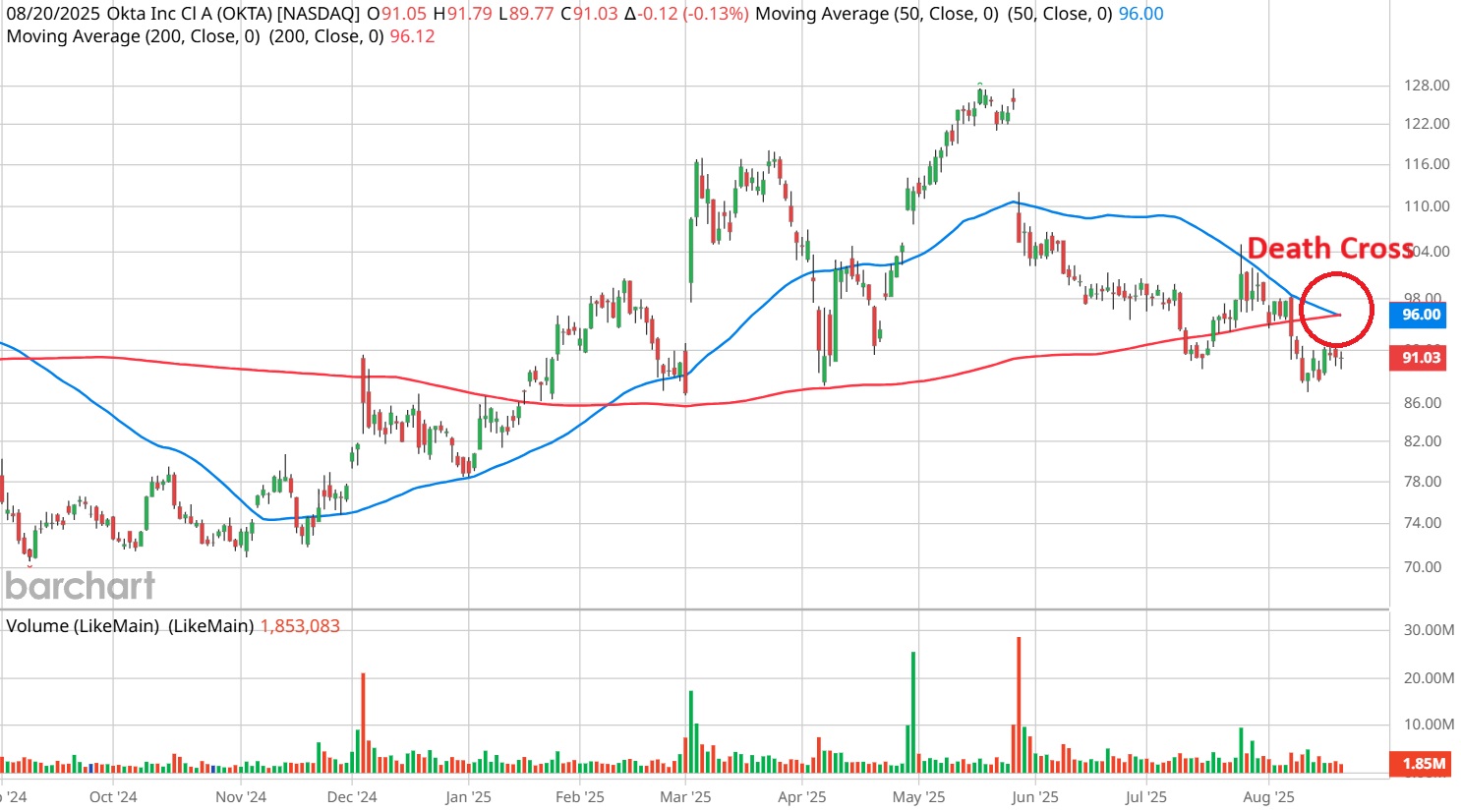
Okta May Have Flashed the Death Cross But Statistical Evidence Points to a Comeback

As a rule of thumb, retail investors tend to avoid publicly traded securities that have flashed the dreaded death cross. A phenomenon where the 50-day moving average crosses below the 200 DMA, the intersection points to sustained weakness for the target security. At the same time, there’s a contrarian philosophy that suggests that because the bearish pressure may have been fully digested, the subsequent moves could be bullish.
Such sentiments align with legendary investor Warren Buffett’s commonly cited aphorism: “Be fearful when others are greedy, and greedy when others are fearful.” This is great and all but it raises an important question — how do you know which ideas are worth pursuing and which ones to avoid?
In my estimation, identity and access management specialist Okta Inc (OKTA) — which recently flashed the death cross — is a prime candidate for a contrarian trade.
On the surface, circumstances don’t look pleasant for OKTA stock. Aside from pinging Barchart’s Death Cross screener, OKTA has effectively earned the ire of the platform’s Technical Opinion indicator, which rates shares as an 88% Sell. Investors are also edgy, with the tech service set to release its second-quarter earnings results on Aug. 26.
Most pressingly, though, OKTA stock has plunged 27% in the past three months, according to Barchart content partner Zacks Investment Research. This sustained negativity has been reflected with the flashing of the death cross — and there doesn’t seem to be much hope that the stock can turn things around.
Not surprisingly (especially with earnings around the corner), the Expected Move calculator provides a massive differential for the Aug. 29 expiration date: the upper price is projected to land at $100.69 while the lower price may fall to $81.37. Of course, the issue here is that there’s no telling which side of the spectrum is more likely to win out.
That’s where a different approach may shed light on the topic.
Using Path Dependency to Narrow Down an Options Strategy for OKTA Stock
Primarily, retail traders — especially those interested in options — utilize volatility-dependent analytics. This approach depends heavily on formulations derived from or influenced by the Black-Scholes model for pricing options. Essentially, the idea is that every optionable stock features a baseline magnitude of volatility. As exogenous factors (such as earnings reports) loom on the horizon, accelerants are baked into the volatility assumptions.
That’s part of the reason why expected move calculators feature conical shapes: the analysis is about estimating a range of pricing possibilities based on volatility calculations. These are also the same calculations that help determine whether an option is cheap or expensive.
However, the challenge is that while an option may be technically cheap relative to volatility expectations, we don’t know which outcome is likelier: the bullish scenario or the bearish. To get a better understanding of how the target security may conditionally move, we can deploy path dependency — using the stock’s actual pricing geometry to estimate where it may end up in the future.
Now, the problem is that conditional probabilities are difficult (if not impossible) to extract because share prices fluctuate wildly. Therefore, we need to impose epistemological continuity in both the input and output variables. To do this, we can treat price action not as scalar signals but as discrete objects or states. In this manner, recurring patterns pop out, allowing for effective analysis.
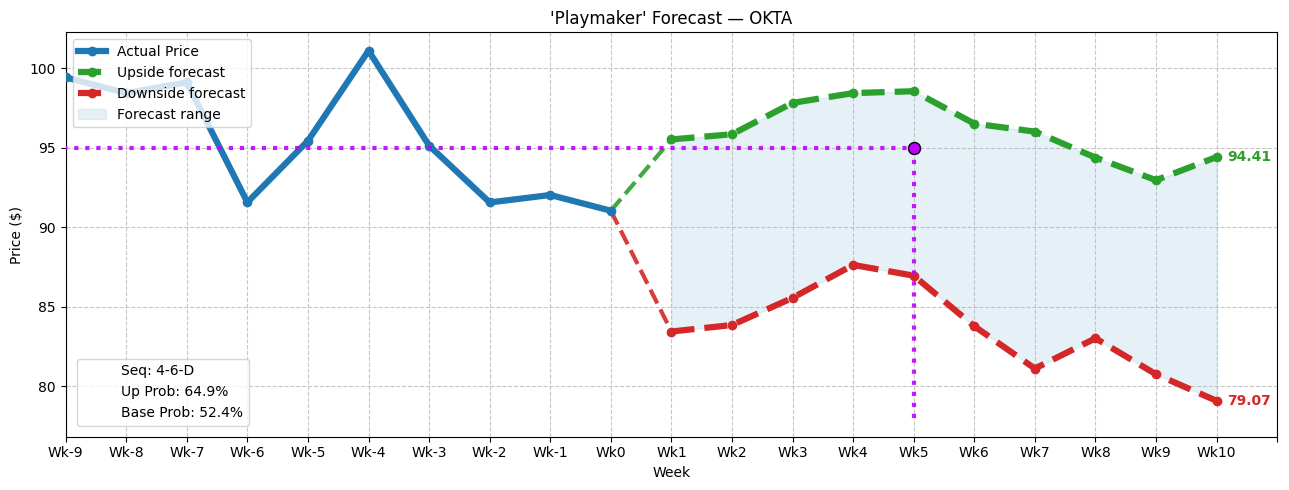
For example, in the trailing 10 weeks, the market voted to buy OKTA stock four times and sell six times. During this period, OKTA incurred a downward trajectory. We can label this discrete state as 4-6-D. Now, we have a falsifiable signal upon which we can conduct probabilistic analysis through the study of past analogs.
Since January 2019, the 4-6-D sequence has flashed 37 times. Notably, in 64.86% of cases, the following week’s price action results in upside, with a median return of 4.93%. As a baseline, the chance that a long position in OKTA stock will rise on any given week is only 52.45%. Therefore, assuming that the implications of the aforementioned sequence pan out, there’s a clear incentive to consider a bullish debit strategy.
At the same time, even if the bulls maintain control of the market over the next 10 weeks, the overall price geometry risks tilting in the negative direction. Subsequently, it may be better to trade OKTA stock rather than view it as a long-term investment opportunity.
Buying Call Spreads the Smart Way
Based on the market intelligence above, arguably the most viable idea is the 92/95 bull call spread expiring Sept. 19. This transaction involves buying the $92 call and simultaneously selling the $95 call, for a net debit paid of $145 (the most that can be lost in the trade). Should OKTA stock rise through the short strike price ($95) at expiration, the maximum profit is $155, a payout of nearly 107%.
Are there higher-paying call spreads available? Yes, in my opinion, you could go for a spread with a short leg of $97.50. One such trade currently features a payout of just over 134%. However, the challenge here is that the delta between the strike price and the positive projected pathway is very tight. Such tightness leaves little margin for error if exogenous factors unexpectedly impact OKTA stock.
Either way, much rides on the empirical reliability of the 4-6-D sequence. Running a one-tailed binomial test reveals a p-value of 0.0881, meaning that there’s only an 8.81% chance that the implications of the signal could materialize randomly as opposed to intentionally.
Given the open and entropic nature of the stock market, that’s a compelling metric to chew on.
On the date of publication, Josh Enomoto did not have (either directly or indirectly) positions in any of the securities mentioned in this article. All information and data in this article is solely for informational purposes. For more information please view the Barchart Disclosure Policy here.